불변 부분 공간(Invariant Subspace) 과 순환 부분 공간(Cyclic Subspace)

불변 부분 공간(T-invariant Subspace) 이란?

교재 내의 정의는 아래와 같다.

정의 벡터공간 V의 선형연산자 T를 생각하자. V의 부분공간 W에 대하여 T(W) $\subseteq$ W 인 W를 V의 T-불변 부분공간(T-invariant Subspace)이라 한다. 즉, 모든 $\mathbf{v} \in $ W에 대하여 $T(\mathbf{v}) \in $ W이다.

즉, 불변 부분 공간은 벡터 공간 V의 부분 공간 중 조금 특이한 부분 공간이라고 생각할 수 있다.

불변 부분 공간이 어떤 점에서 특이하다고 할 수 있을까? W를 벡터 공간 V의 부분 공간이라고 해보자. 벡터 공간 W에서 임의의 원소 벡터 w 를 뽑고, 이 벡터 w 를 이용해 T(w) 를 구했을 때, 이 T(w) 가 항상 W 안에 항상 속해 있다는 보장은 할 수 없다. W는 V의 부분 공간일 뿐이므로, W를 제외한 다른 영역으로 매핑 될 가능성이 충분하다.

하지만, 임의의 원소 벡터 w를 벡터 공간 V나 일반적인 부분 공간 W가 아닌, 불변 부분 공간이라고 정의 되어 있는 부분 공간 W’에서 추출했다고 가정하면 얘기가 달라진다. 불변 부분 공간의 정의에 따라 T(v) 는 항상 불변 부분 공간 W 내의 벡터와 매핑 된다.

그니까, 정말 요약해보면, 불변 부분 공간 내의 벡터는 선형 연산자 T를 통해 보내도 결국 불변 부분 공간내의 벡터와 매핑된다는 의미이다.

어라? 선형 연산자를 통해 태워서 보냈는데도 결과값이 같은 부분 공간의 벡터와 매핑이 된다고? 아! 그래서 ‘불변’이라고 하는구나… 불변….비슷한 개념으로 뭔가 있었던 것 같은데..? 아! 고윳값과 고유벡터가 있겠구나! 실제로 현재 공부 중인 교재(아래 Reference 참고)에서는 고윳값과 고유벡터를 설명하는 챕터에서 불변 부분 공간이 등장 한다.

불변 부분 공간의 예시

어떤 공간을 불변 부분 공간이라고 할 수 있을까?

1. 대표적으로는 {$\mathbf{0}$}, 즉, 제로 벡터만을 포함한 집합이 있다. 모든 벡터 공간에 제로 벡터가 포함 되어 있는 것은 자명한 사실이고, 벡터 공간의 선형성으로 인해, 제로 벡터만 있는 집합은 부분 공간이자 곧 불변 부분 공간이다.(선형 연산자에 제로 벡터를 넣을 경우 제로 벡터가 나오기 때문에)

2. 또 다른 예시로는 커널(kernel)이 있다.

(이미지 출처 : http://mathonline.wikidot.com/invariant-subspaces)

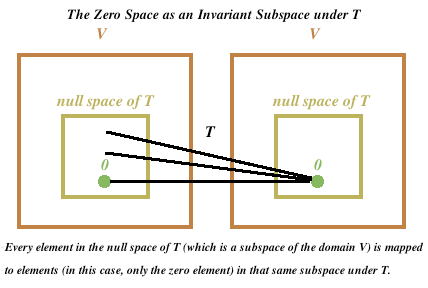
• 커널은 그 정의에 따르면, 정의역의 원소 중 선형연산자의 결과값이 모두 제로 백터와 대응 되는 원소들의 집합이다. (즉, 다음과 같다. ${\mathbf{v} \in V : T\mathbf{v = 0}}$)
• 커널 역시 부분 공간이므로, 제로 벡터를 포함하고 있고, 커널의 정의에 따라 커널에서 뽑은 임의의 원소는 모두 제로 벡터와 매핑 된다. 즉, 불변 부분공간의 정의를 모두 만족하고 있으므로, 커널도 불변 부분 공간이다.

1. 마지막 예시로는 고윳값과 고유 벡터 챕터 에서 등장한 개념인만큼 고유 공간(eigen space) 또한 불변 부분 공간이다.

순환 부분 공간(T-Cyclic Subspace)이란?

역시 교재 내의 정의를 먼저 살펴보자.

정의 벡터공간 V의 선형연산자 T와 영이 아닌 벡터 $\mathbf{x} \in V$ 에 대하여 다음과 같은 부분공간 W를 $\mathbf{x}$ 에 의해 성생된 (V의) T-순환 부분공간(T-cyclic subspace) 이라 한다. \(W = span({\mathbf{x}, T\mathbf{x}, T^2\mathbf{x}, \ldots})\)

위 내용을 토대로 정의된 순환 부분 공간은 위에 언급 되었던 불변 부분공간이기도 한데, 그 내용은 아래와 같다.

W를 $\mathbf{x} \in $ V 에 의해 생성된 순환 부분공간이라고 하자

\[\mathbf{w} \in W, \mathbf{w} = \sum_{i=1}^\infty a_iT^i\mathbf{x} \rightarrow T\mathbf{w} = \sum_{i=1}^\infty a_iT^{i+1}\mathbf{x} \in W\]

순환 부분 공간 W에서 임의의 원소 w를 뽑았고, w를 기저의 벡터들을 이용해 선형 결합으로 표현하였다(화살표 왼쪽). 그리고 Tw 의 선형 결합 또한 W의 기저의 벡터들의 선형 결합으로 표현할 수 있다는 사실을 알았다.(화살표 오른쪽) 즉, Tw가 W에 속해 있다는 것을 알았다. 따라서 순환 부분 공간 W는 불변 부분 공간이기도 하다.

순환 부분 공간은 그 쓰임새가 다양한데, 특성 다항식을 이용하지 않고도, 행렬의 고윳값과 고유벡터를 구할 수 있는 케일리-해밀턴 정리(Caley-Hamilton Theorem)이 그 예이다.

T-순환 부분 공간과 관련된 정리

정리 유한차원 벡터 공간 V의 선형연산자 T와 영이 아닌 벡터 $\mathbf{v} \in $ V 에 의해 생성된 T-순환 부분공간 W를 생각하자. k = dim(W) 라 하면 다음이 성립한다.

(1) {$\mathbf{v}$, T($\mathbf{v}$), T^2($\mathbf{v}$), $\ldots$, T^(k-1)($\mathbf{v}$)}는 W의 기저이다.
(2) $a_0\mathbf{v} + a_1T(\mathbf{v}) + \cdots + a_{k-1}T^{k-1}(\mathbf{v}) + T^k(\mathbf{v}) = 0$ 이면, $T_W$ 의 특성 다항식은 f(t) = $(-1)^k(a_0 + a_1t + \cdots + a_{k-1}t^{k-1} +k^t)$이다.

우선 위 정리에서 (1)이 좀 처럼 이해가 되질 않았었는데, 포스팅을 하려고 정리하다 보니 이해가 된 것 같다. 일단 이해가 되지 않았던 부분은, (1)의 내용이 W의 기저가 {$\mathbf{v}$, T($\mathbf{v}$), T^2($\mathbf{v}$), $\ldots$, T^(k-1)($\mathbf{v}$)} 라는 것을 굳이 증명을 해야하나…? 라는 생각이 들었다. 왜냐하면 저 벡터들을 스팬한 걸 T-순환 부분공간이라고 정의했는데, 왜 그게 증명할 거리라고 생각했지? 라고 이해했기 때문이다.

하지만, 자세히 들여다보니, 정리 5.21의 (1)에는 이전에 T-순환 부분 공간을 처음 설명할 때에는 없었던, $T^{k-1}$ 이 존재하더라. 그니까, 정의에는 $(T^0, T^1, T^2, \ldots, )$ 식으로 집합 내 선형 연산자의 승수가 제한이 없었는데,(1)에서는 k=dim(W) 이라 할 때, k-1로 명확하게 정의가 되어있었다. 정의와 정리 5.21의 (1)에서의 차이는

1. 정의에서는 유한차원이 보장되어 있지 않고,
2. 정리 5.21에서 V를 유한차원으로 가정했다고 하더라도, {$\mathbf{v}$, T($\mathbf{v}$), T^2($\mathbf{v}$), $\ldots$, T^(k-1)($\mathbf{v}$)}가 W의 기저인 것은 당연하지 않다는 것이다.

1번은 명확하고, 2번은 아래와 같은 의미이다.(물어서 답변 받은 내용 정리)

• spanning set에 있는 벡터가 T를 계속 먹이면서 지수가 커지고 있는데, 앞에 있는 벡터부터 순서대로 일차 독립이 보장되다가 어느 순간 종속적이 된다는 것은 너무 쎈 가정이다. 우리는 spanning set의 벡터 중에서 독립적인 벡터 subset만 추리면 기저가 된다는 것을 아는데, 그 일부가 반드시 앞에서부터 이루어 져야 한다는 것은 보장된 바가 없음

• 극단적으로 3차원이라고 했을 때, v, T^3v, T^4v 이렇게 되면…? Tv, T^2v는 종속이어서 뺀다면..?

• 그래서 사실 정의만 봐서는 쟤네들이 span 하는건 맞지만 그 중 어떤 애들이 서로 독립적일지는 모르는데,

• 정리에서 주장하는 바는 순서대로, 앞에서부터 독립적이라는 것을 보장하기 때문에 정리가 non-trivial 한 것!

처음에 이해가 되지 않던 부분은 이해가 되었으니, 이제 (1)에 대한 증명을 이해해 봐야겠다.

이 정리의 핵심은, 다음과 같다.(역시 물어봐서 답변 받는 내용 정리)

• 우선 기저라고 주장하는 벡터 셋인 $ \{\mathbf{v}, T(\mathbf{v}), T^2(\mathbf{v}), \ldots, T^{j-1}(\mathbf{v}) \}$ 를 $\mathfrak{B}$라고 하자.

• j-1에서 j의 범위를 1부터 하나씩 늘려가면서, 해당 벡터 셋의 독립성을 확인한다. 그리고 증명에서 가정하는 바와 같이 $\mathfrak{B}$ 이 일차 독립을 유지하는 가장 큰 자연수 j를 잡는다.

• 일단 $\mathfrak{B}$의 구성이 spanning set의 subset이라는게 가장 중요하고,

• 그 와중에 그 j가 정확히, 딱, k이다.(즉, j=k)

• 그러면 spanning set의 부분집합인데, 일차 독립이면서 원소의 수가 딱 dim. 과 동일하네? –> 이래서 basis가 된다!

위의 내용은 증명의 전체적인 흐름이고, 증명에서 전개하는 바는 아래와 같다.

• $\mathfrak{B}$ 의 독립성을 유지하면서 늘릴 수 있을 때까지 새로운 벡터 $T^{j-1}(\mathbf{v})$를 하나씩 추가하기 때문에, 가정에 의하면, $\mathfrak{B}$의 독립성은 깨지지 않는다.

• 따라서 $\mathfrak{B}$을 벡터들을 이용해 $a_0v + a_1T(\mathbf{v}) + \cdots + a_{j-1}T^{k-1}(\mathbf{v}) + a_jT^{k}(\mathbf{v}) = 0$ 와 같은 선형 결합을 생각해보면, $a_j$는 0이 될 수 없다. $a_j$가 0이 되는 순간 j가 $\mathfrak{B}$ 의 독립성을 유지하는 가장 큰 자연수라는 가정이 위배 되기 때문이다.

• $a_j$가 0이 아니므로, 위의 선형 결합을 $a_jT^{k}(\mathbf{v})$를 제외하고 모두 이항할 수 있고, 이는 아래와 같이 표현될 수 있다.

\[T^{j}(\mathbf{v}) = a_{j}^{-1}(a_0v + a_1T(\mathbf{v}) + \cdots + a_{j-1}T^{k-1}(\mathbf{v}))\]

• 이는 결국, $T^{j} \in \mathfrak{B}$ 임을 의미한다.

• 따라서 Span($\mathfrak{B}$) 는 T 불변 부분공간이고, $\mathbf{v} \in $Span($\mathfrak{B}$) 이다.

• W는 $\mathbf(v)$를 포함하는 가장 작은 T 불변 부분 공간이므로 W와 $Span($\mathfrak{B}$)가 서로 double inclusion임을 알 수 있다.

그리고 (2) 번의 증명은,

\(a_0\mathbf{v} + a_1T(\mathbf{v}) + \cdots + a_{k-1}T^{k-1}(\mathbf{v}) + T^{k}(\mathbf{v}) = 0\) 을 만족하는 스칼라 $a_0, a_1, \cdots , a_{k-1}$ 이 존재한다면, $T_W$의 특성 다항식은 $f(t) = (-1)^{k}(a_0 + a_1t + \cdots + a_{k-1}t^{k-1} + t^k)$ 이라는 의미이다.

• (1)에서 스칼라 $a_0, a_1, \cdots , a_{k-1}$ 이 존재하는 것을 보인 것이나 마찬가지 이기 때문에, $T_W$의 행렬 표현식을 구하고, 이를 이용해 특성다항식을 구하면 $f(t) = (-1)^{k}(a_0 + a_1t + \cdots + a_{k-1}t^{k-1} + t^k)$ 임을 확인할 수 있다.

그래서 이거 어디 쓰이지…?

신나게 증명을 이해하려고 노력하고, 결국 이해하면 그래서 이게 어디에 쓰이는거지…? 라는 생각이 든다.

알아본 바로는 아래와 같은 부분에서 연관이 있다.

1. 고유 공간은 결국 T 불변 부분공간이다. 대각화 가능한 행렬을 고유 분해하면, 고유 공간끼리의 직합으로 구성할 수 있으므로, T 불변 부분 공간을 이해하는 것은 행렬의 특징을 잘 이해할 수 있는 방법 중에 하나란 말이 된다.

2. 위 정리를 이용해 케일리 해밀턴 정리를 증명하는데 쓰인다. 케일리 해밀턴 정리는 계산을 간편화하거나 혹은 조던 캐노니컬 폼에 쓰이기 때문에 매우 중요하다. (사실 조던 캐노니컬 폼은 아직 공부 안해서 케일리 해밀턴 정리가 얼마나 크리티컬하게 적용되는지 잘 모르겠다)

마무리하며…

사실 정말 어려운 부분이고, 이해도 어려웠던 부분인데 같이 스터디를 하는 스터디원들 덕분에 어느 정도 이해할 수 있게 된 것 같다. 시간을 많이 들인 거 치고 실무에서 적용할 만한 부분이 많이 보이지는 않지만, 선대가 또 언제는 안 그랬던가…. 수리적 사고 방식이 좋아졌다고 위로하며, 나중에 또 보게 될 경우를 위해 기록을 남겨놓은 것으로 마무리해야겠다.

Reference - 스티븐 H.프리드버그, 아놀드 J.인셀, 로렌스 E, 스펜스, 『프리드버그 선형대수학 5판』,한빛 아카데미(2020)