Dongsu Kang

Data Analyst

통계학에서의 bootstrap에 대해 정리해보자

3 minute read

BootStrap이란?

  • BootStrap 은 확보한 데이터에서 복원 추출로 Sampling 하는 방법이다.
  • 복원 추출을 통해 simulated sampled 을 만든다고 할 수 있다.
  • 모수를 추론하기 위해 사용한다.

BootStrap 은 어떻게 하는 걸까?

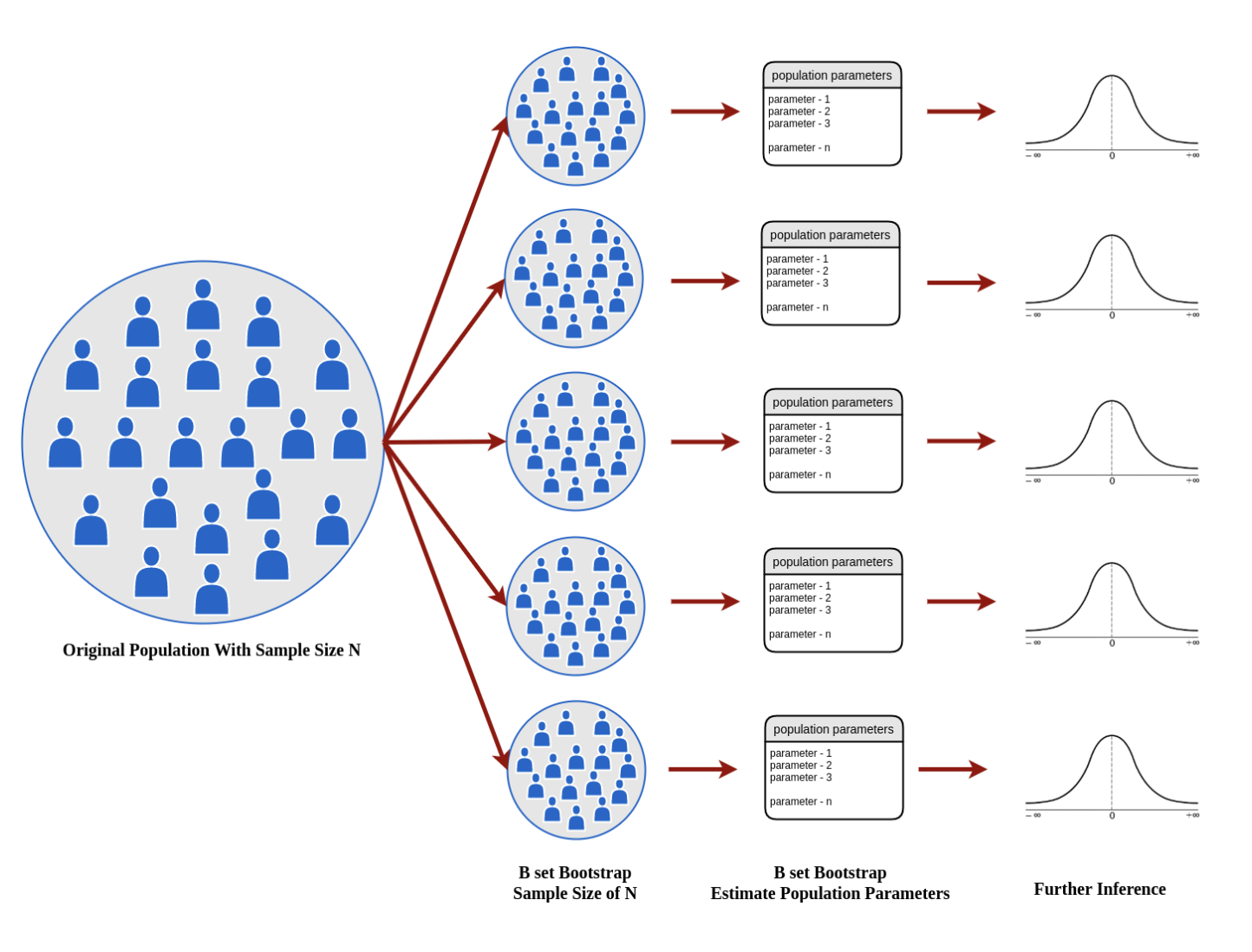
(이미지 출처 : https://arifromadhan19.medium.com/resampling-methods-a-simple-introduction-to-the-bootstrap-method-3a36d076852f)
  1. 가지고 있는 데이터에서 N 개의 샘플을 랜덤 추출한다. 이 때 복원 추출로 뽑는다.
  2. 1번에서 뽑은 샘플에서 통계량을 구하고 이를 킵한다.
  3. 1,2번을 반복한다.
  4. 통계량의 분포를 확인한다.

BootStrap 을 왜 하는 걸까?

  • 통계를 이용해 우리가 하고 싶은 것은, 샘플을 통해 모수를 추정하는 일이다.
  • 모수를 추정하기 위해 사용하는 것은, 통계량인데, 이 통계량의 의미는 요약하면 ‘표본의 특징을 수치화한 값’이다. 보통 평균이나 분산을 사용한다.
  • 모수를 추정하는 방법에 아는 방법은 점 추정과 구간 추정 두 가지가 있는데, 그 중 구간 추정을 많이 사용한다.
    • 예를 들어 샘플의 평균을 이용해 모평균을 추정한다고 하면,
      • 점 추정은 ‘모집단의 평균이 정확히 2.3’이다 라고 하는 것이고,
      • 구간 추정은 ‘모집단의 평균이 1.7과 2.8사이에 있을 확률이 90%이다’ 라고 하는 것인데
      • 점 추정의 방법과 같이 모집단의 평균을 정확하게 맞추는 것은 어렵다. 그래서 구간 추정을 많이 사용한다.
  • 그런데 문제가 있다. 모집단의 구간을 추정하려면, 모집단의 분포를 알아야 한다.
    • 학교를 다닐 때 다음과 같은 공식을 본 적이 있을 것이다. $\bar{X} \pm Z_{\alpha/2} \frac{s}{\sqrt{n}}$
    • 여기서 $\alpha$에 따라 $Z_{\alpha/2}$가 결정되는데, 이 $Z_{\alpha/2}$는 분포표를 보고 찾았다.
    • 그리고 이 분포표는 모집단의 분포에 따라 바뀐다. 예를 들어 모집단이 정규 분포라면 정규 분포표를, 카이제곱 이라면 카이제곱 분포표를 보고 찾았다.
  • 하지만, 현실의 데이터에서는 모집단의 분포를 가정할 수 없는 경우가 대부분이다.
  • 이러한 경우에 우리는 bootstrap 을 이용해, 모집단의 신뢰 구간을 추정할 수 있다.

BootStrap 으로 어떻게 모집단 신뢰 구간을 추정을 할 수 있을까?

  • (아래 내용이 확실하게 증명된 사항인지는 알 수 없고, 그냥 뇌피셜이다.)
  • 통계학에서는 우리가 얻은 데이터를 모집단의 일부를 반영하는, 랜덤하게 추출한 샘플로 본다.
  • 즉, 우리의 데이터의 적당히 큰, 일부 데이터를 계속 뽑는 것은 결국 모집단에서 데이터를 계속 뽑는 것이라는 이야기 이다.

  • 그렇게 우리는 bootstrap을 반복할 때 마다 모집단의 분포에 가까워진다고 볼 수 있다.

  • 아래 그림을 통해 세부적으로 이해할 수 있다.

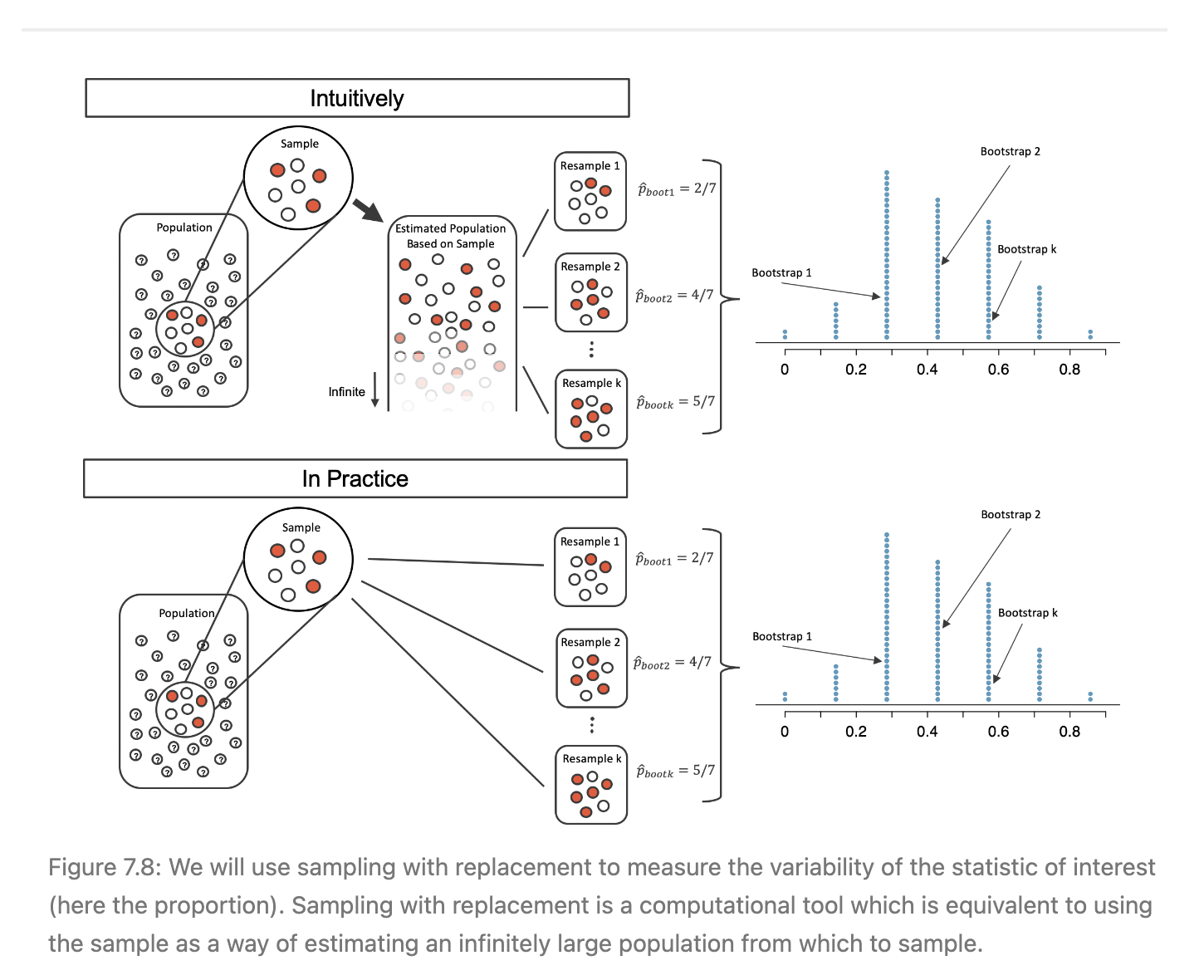
(이미지 출처 : https://bookdown.org/gregcox7/ims_psych/foundations-bootstrapping.html)
  • 먼저 그림의 Intuitively 를 보자
    • 이 부분은 직관적인 이해를 돕기 위해 만들어진 듯 하다.
    • 모집단에서 샘플을 뽑았고, 이 샘플 하얀색 공 4개와 빨간색 공 3개로 이루어져 있다.(모집단에서 샘플을 제외한 공의 색깔은 알 수 없다.)
    • 7개의 하얀색, 빨간색이 섞인 공의 샘플을 통해 모집단을 추정하면, Estimated Population Based on Sample 과 같은 형태가 될 것이다.
    • 이 모집단에서 다시 7개의 샘플을 뽑는 작업을 여러 번 반복한다.(즉, resample 한다.)
    • 각각의 7개 짜리 샘플들에서 나온 통계량을 기록한다. 여기서는, 하얀색 공이 나올 비율이라고 한다.
    • 이 기록들이 쌓이고 쌓여서, 하나의 표본 분포를 만들어낸다.
  • 다음은 In Practice 를 보자
    • 이 부분은 실제로 코드단에서 구현되는 것을 그림으로 설명한 듯 하다
    • Intuitively와 다른 점은 처음 모집단에서 뽑은 샘플을 통해 stimated Population Based on Sample 을 만들지는 않는다. 바로 resample 을 한다.
    • 그리고 각각의 resample 된 샘플을에서 나온 통계량을 기록한다.
    • 이 기록들이 쌓이고 쌓여서, 하나의 표본 분포를 만들어낸다.
    • 그 결과, Intuitively 와 파트처럼 stimated Population Based on Sample 을 만들고 resample 을 하는 것과 같은 표본 분포가 만들어진다.

(이미지 출처 : https://bookdown.org/gregcox7/ims_psych/foundations-bootstrapping.html)
  • 이렇게 resample 된 샘플들에서 얻은 통계량의 분포로 만들어낸 표본 분포에서 우리는 bootstrap percentile confidence interval 을 얻을 수 있다.
  • 해석하면, 위의 이미지에서는 모수에서 샘플을 100번 뽑을 때, 하얀색 공의 비율이 0%부터 11.3% 사이인 경우가 95% 나온다는 의미이다.

BootStrap 파이썬 코드로 구현하기

results = []
for nrepeat in range(1000):
    sample = resample(sample_statistics)
    results.append(sample.median())
results = pd.Series(results)
print('Bootstrap Statistics:')
print(f'original: {sample_statistics.mean()}')
print(f'bias: {results.mean() - sample_statistics.median()}')
print(f'std. error: {results.std()}')


print(frequency.mean())
np.random.seed(seed=3)  
sample20 = resample(frequency, n_samples=10000, replace=False)
print(sample20.mean())
results = []
for nrepeat in range(500):
    sample = resample(sample20)
    results.append(sample.mean())
results = pd.Series(results)

confidence_interval = list(results.quantile([0.05, 0.95]))

ax = results.plot.hist(bins=30, figsize=(14, 14))
ax.plot(confidence_interval, [55, 55], color='black')
for x in confidence_interval:
    ax.plot([x, x], [0, 65], color='black')
    ax.text(x, 70, f'{x:.0f}', 
            horizontalalignment='center', verticalalignment='center')
ax.text(sum(confidence_interval) / 2, 60, '90% interval',
        horizontalalignment='center', verticalalignment='center')

meanIncome = results.mean()
ax.plot([meanIncome, meanIncome], [0, 50], color='black', linestyle='--')
ax.text(meanIncome, 10, f'Mean: {meanIncome:.0f}',
        bbox=dict(facecolor='white', edgecolor='white', alpha=0.5),
        horizontalalignment='center', verticalalignment='center')
ax.set_ylim(0, 80)
ax.set_ylabel('Counts')

plt.tight_layout()
plt.show()

Reference

  • https://ko.wikipedia.org/wiki/%ED%86%B5%EA%B3%84%EB%9F%89
  • https://statisticsbyjim.com/hypothesis-testing/bootstrapping/
  • 파이썬 코드 출처 : https://github.com/gedeck/practical-statistics-for-data-scientists

You may also enjoy