다양한 확률 분포들의 이론 및 Scipy를 이용한 실습

이산형 확률 분포

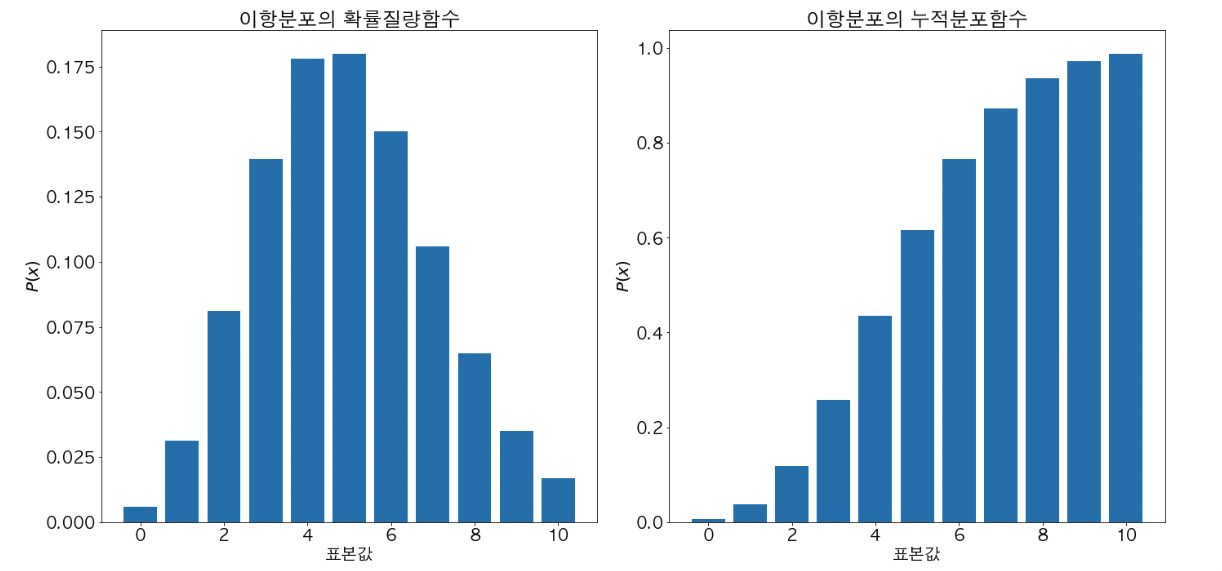
이항 분포

• 실험 또는 시행의 결과가 참/거짓, 1/0, 성공/실패 등 두 가지로만 나오는 시행을 베르누이 시행 이라고 한다.
• 베르누이 시행을 n번 했을 때, k번 성공할 확률에 대한 이산형 확률 분포이다.
• 이항 분포의 모수는 성공 확률 p와 시행 횟수 n이다. 이 때, 성공 확률 p는 일정하다고 가정한다.
• 이항 분포를 통해 아래와 같은 질문의 답변을 할 수 있다.
  • 시행의 결과가 성공 또는 실패로 구분할 수 있는 경우, 100번 시행했을 때 5번 성공할 확률은 얼마인가? 또는 5번 이하로 성공할 확률은 얼마인가?
• 이항 분포의 대의적 정의는 아래와 같다.

\[X \sim B(n, p) \ \Leftrightarrow \ X \overset{d}{\equiv} Z_1 + Z_2 + \cdots + Z_n, \ Z_i \overset{iid}{\sim}Bernoulli(p)(i=1, \cdots, n)\]

• 확률 변수 X가 이항분포를 따른다면 아래와 같이 표기한다.

\[X \sim Bin(x; n, \mu)\]

Scipy 코드

import scipy as sp 
n = 100
rv = sp.stats.binom(n, p)

plt.figure(figsize=(20, 10))

plt.subplot(1, 2, 1)
xx = np.arange(N/10+1)
pmf = rv.pmf(xx)
plt.bar(x=xx, height=pmf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("이항분포의 확률질량함수")


plt.subplot(1, 2, 2)
xx = np.arange(N/10+1)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("이항분포의 누적분포함수")


plt.tight_layout()
plt.show()

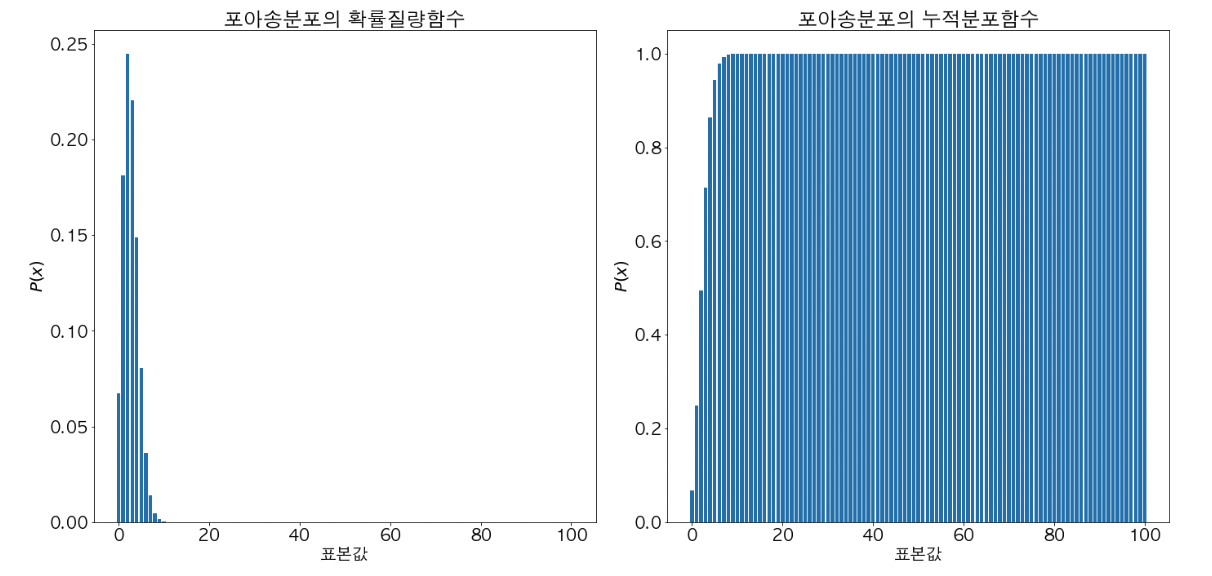
포아송 분포

• 확률 변수 X가 이항 분포를 따를 때, 시행 횟수 N이 무수히 크고, 성공 확률 p 가 충분히 작을 때, 이항 분포를 포아송 분포로 근사할 수 있다.
• 포아송 분포는 일정한 시간(단위 시간) 또는 공간(단위 공간) 내에서 발생하는 사건의 발생 횟수에 따른 확률이다.
  • 즉, 단위 시간동안 n 번 발생했을 때, 그 다음 단위 시간동안 x 번 발생할 확률
  • 예를 들어 콜센터에 걸려오는 전화의 수가 평균 1분당 2회
  • 지난 시즌에서 100타석 당 홈런을 2개 친 야구 선수가 금년에 400타석에서 15개의 홈런을 칠 확률
  • 강이나 하천에서 일정한 부피의 물에 존재하는 부유생물의 수
  • 일정한 시간 동안 컴퓨터 서버에 요청되는 접속 횟수
• 포아송 분포를 통해 아래와 같은 질문의 답변을 할 수 있다.
  • 콜센터에 걸려오는 전화의 수가 평균 1분당 2회일 때, 10분 동안 5번 전화가 올 확률은?
  • 한 달에 발생하는 토네이도 횟수가 18회 일 때, 하루에 토네이도가 발생할 확률은?
• 포아송 분포는 모수로써 발생률(occurrence rate) $\lambda$를 가지는데, $\lambda$는 이항분포의 np를 근사하여 얻었다는 것을 전제로 한다.
  • 발생률이라고 표현하여 직관적으로는 비율처럼 보이지만, $\lambda$의 예시로는 평균 분당 발생 횟수 등의 평균을 사용한 예시를 더 많이 보았다.
• 아래와 같은 조건이 만족되면 발생률 $\lambda$인 포아송 과정(Poisson process)라고 한다.
  • 정상성(Stationarity) : 현상이 발생하는 횟수의 분포는 시작하는 시각에 관계없다. 즉, 언제 시작해도 발생하는 횟수는 같다. 시간대에 따라 발생 횟수가 달라지지 않는다.
  • 독립증분성(Independent increment) : 시각 0부터 t까지 현상이 발생하는 횟수와 시각 t 후부터 t+h까지 발생하는 횟수는 서로 독립이다.
  • 비례성(Proportionality) : 짧은 시간 동안에 현상이 한 번 발생할 확률은 시간에 비례한다.
  • 희귀성(Rareness) : 짧은 시간 동안에 현상이 두 번 이상 발생할 확률은 매우 작다.
• 발생률이 $\lambda$인 포아송과정에서 발생 횟수의 분포는 평균이 $\lambda t$인 포아송 분포이다. 즉,

\[N \sim Poisson(\lambda t)\]

Scipy 코드

import scipy as sp 

poission_lambda = prob

N = 1000
mu = 0.05
rv = sp.stats.poisson(mu)

plt.figure(figsize=(20, 10))

plt.subplot(1, 2, 1)
xx = np.arange(N/10+1)
pmf = rv.pmf(xx)
plt.bar(x=xx, height=pmf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("포아송분포의 확률질량함수")


plt.subplot(1, 2, 2)
xx = np.arange(N/10+1)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("포아송분포의 누적분포함수")


plt.tight_layout()
plt.show()

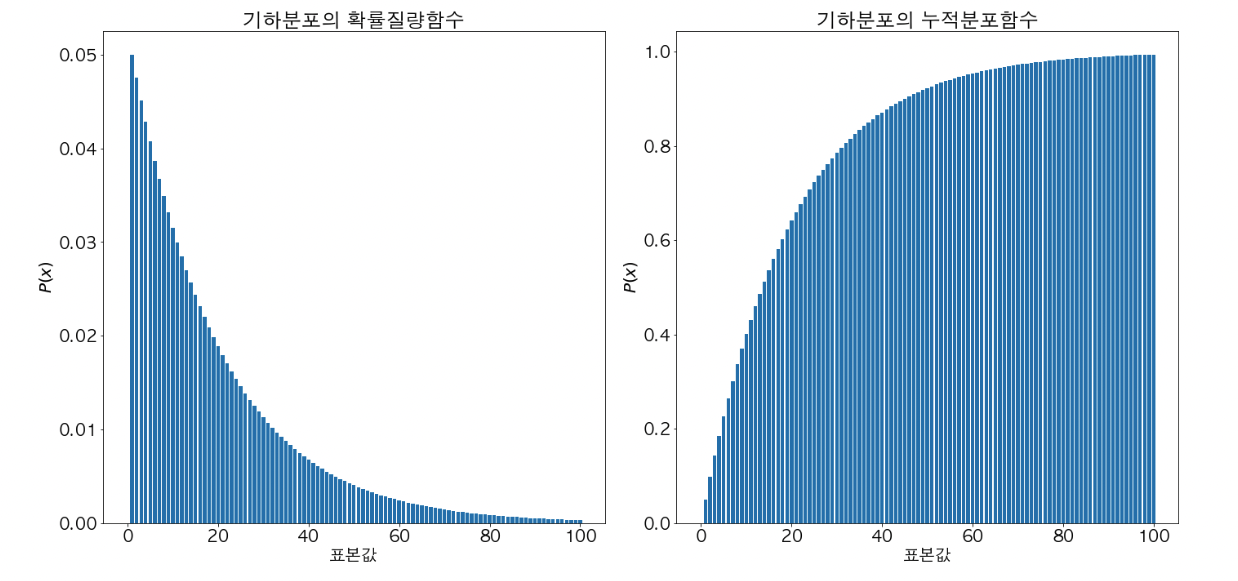
기하 분포

• 기하 분포는 서로 독립이고 성공률이 p 인 베르누이 시행의 결과값을 확인했을 때, 첫 번째 성공할 때까지의 시행 횟수 별 확률을 나타내는 확률 분포 이다.
  • 말이 어려운데, pdf에서 x 축이 n 번 시행 횟수이고, y 축은 n 번 시행 했을 때 첫 번째 성공을 관측할 확률이다.
• 기하 분포는 모수로써 성공 확률 p 를 가진다.
• 기하 분포를 통해 아래와 같은 질문의 답변을 할 수 있다.
  • 유저에게 문자 메세지를 날려 앱에 유입을 유도하는 행위가 서로 독립적인 베르누이 시행이라고 했을 때, n명에게 날려 1명이 유입될 확률은?
• 기하 분포는 성공 횟수가 1인 음이항 분포와 분포적으로 동일하다.

Scipy 코드

import scipy as sp
p=0.05
rv = sp.stats.geom(p)

plt.figure(figsize=(20, 10))

plt.subplot(1, 2, 1)
xx = np.arange(N/10+1)
pmf = rv.pmf(xx)
plt.bar(x=xx, height=pmf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("기하분포의 확률질량함수")


plt.subplot(1, 2, 2)
xx = np.arange(N/10+1)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("기하분포의 누적분포함수")


plt.tight_layout()
plt.show()

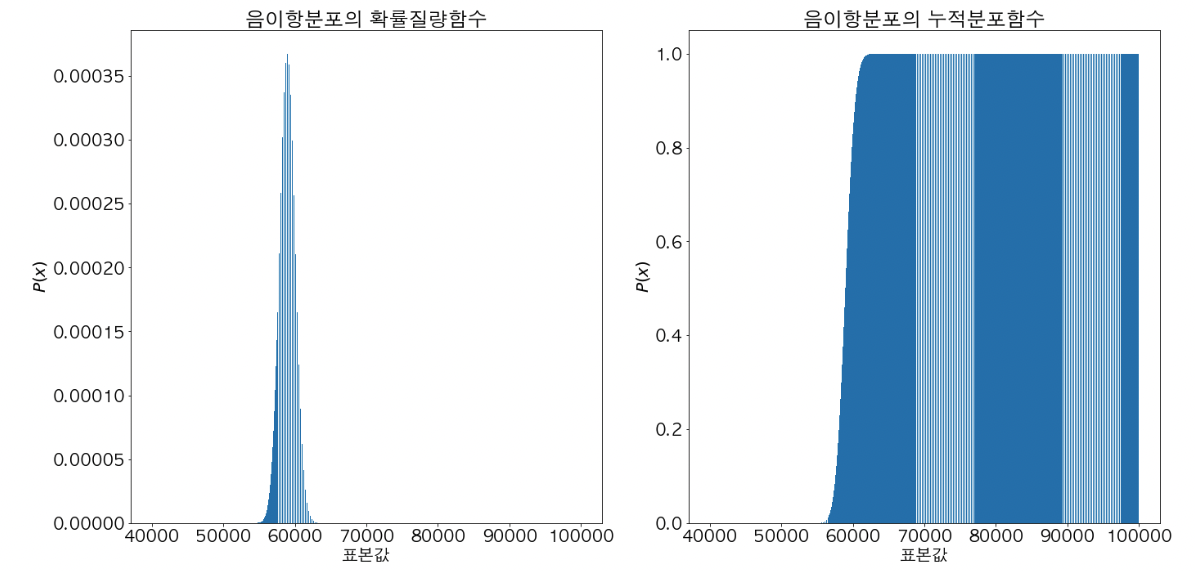
음이항 분포

• 음이항 분포는 서로 독립이고 성공 확률이 p인 베르누이 시행의 결과값을 확인했을 때, r 번째 성공까지의 시행 횟수 별 확률을 나타내는 확률 분포이다.
  • pdf에서 x 축이 n 번 시행 횟수이고, y 축은 n 번 시행 했을 때 r 번 성공을 관측할 확률이다.
• 음이항 분포의 모수는 목표로 하는 성공 횟수 r 과 성공 확률 p 이다.
• 음이항 분포를 통해 아래와 같은 질문의 답변을 할 수 있다.
  • 유저에게 문자 메세지를 날려 앱에 유입을 유도하는 행위가 서로 독립적인 베르누이 시행이라고 했을 때, n명에게 날려 r명이 유입될 확률은?
• 음이항 분포의 대의적 정의 \(X \sim Negbin(r, p) \ \Leftrightarrow \ X \overset{d}{\equiv} Z_1 + Z_2 + \cdots + Z_n, \ Z_i \overset{iid}{\sim}Geo(p)(i=1, \cdots, n)\)

Scipy 코드

# n is number of success
# p is the probability of single success
p = 0.05
n = 3103
rv = sp.stats.nbinom(n=n, p=p)

plt.figure(figsize=(20, 10))

plt.subplot(1, 2, 1)
xx = np.arange(40000, 100000)
pmf = rv.pmf(xx)
plt.bar(x=xx, height=pmf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("음이항분포의 확률질량함수")


plt.subplot(1, 2, 2)
xx = np.arange(40000, 100000)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("음이항분포의 누적분포함수")


plt.tight_layout()
plt.show()

초기하 분포

• 크기가 N인 모집단에서 타겟팅 대상이 K개 있다고 했을 때, 비복원추출 로 n개를 골랐을 때, 그 중 K개 안에서 k 개가 뽑힐 확률
• 초기하 분포에서 n 개를 추출하는 행위를 비복원추출이 아닌 복원 추출로 할 경우, 이는 곧 이항 분포와 동일하다.
• 생각해보면 초기하 분포의 application 적인 측면은 아래 2가지가 만족되어야 한다.
  • 비복원추출이어야 하는 경우
  • 범위가 크게 2개가 있어야 한다.
    • 전체 N개 안에서 K개라는 boundary가 필요
    • 즉, 모집단이 한정되어 있어야 하고, 시행이 그 모집단 내에서 이루어져야 한다.
• 초기하 분포를 통해 아래와 같은 질문의 답변을 할 수 있다.
  • 한 유저가 좋아요 한 상품이 20개가 있다고 가정한다. 이 중 프로모션을 진행하는 상품이 7개가 있다.
  • 이 유저가 좋아요 한 상품들 중 3개를 구매할 때, 프로모션을 진행하는 상품을 1개이상 구매할 확률은?
  • N=20, K=7, n=3, k=1 로 정리할 수 있음

Scipy 코드

# Suppose we have a collection of 20 animals, of which 7 are dogs. 
# Then if we want to know the probability of finding a given number of dogs if we choose at random 12 of the 20 animals, 
# we can initialize a frozen distribution and plot the probability mass function: [M, n, N] = [20, 7, 12]
M, n, N = 20, 7, 3
rv = sp.stats.hypergeom(M=M, n=n, N=N)

plt.figure(figsize=(20, 10))

plt.subplot(1, 2, 1)
xx = np.arange(n+1)
pmf = rv.pmf(xx)
plt.bar(x=xx, height=pmf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("초기하분포의 확률질량함수")


plt.subplot(1, 2, 2)
xx = np.arange(n+1)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("초기하분포의 누적분포함수")


plt.tight_layout()
plt.show()

연속형 확률 분포

• 연속형 확률 분포부터는 cdf 를 이용해서 확률을 구해야 한다.
  • 연속형 확률 분포에서는 이산형 확률 분포와 달리 점 추정식의 시점에 대한 확률을 구할 수 있다.

지수 분포

• 어떤 사건이 발생하고, 다음 사건이 발생하기까지의 대기시간이 얼마나 될 것인가?
  • 단, 사건의 발생 횟수는 포아송 분포를 따라야 한다.
  • 이 경우 사건의 대기시간이 지수분포를 따른다고 할 수 있다.
• 지수 분포의 무기억성
  • 어떤 핸드폰을 구매 시점 이후로 5년이 지나면 고장날 확률이 90%라고 하자.
  • 핸드폰을 2년 사용했고, 한 번도 고장 나지 않았다고 해도, 이 핸드폰의 고장 확률은 5년이 지나면 90%로 똑같다.

  • t = 5년, $P(X>t)$ = 90%, a = 2년 $P(X > a+t

    X > a)$ 도 90%. 즉, 같다

\[P(X > a+t| X > a ) = P(X > t)\]

• 지수 분포의 모수는 1/$\lambda$ 이다. 여기서 $\lambda$ 는 포아송 분포의 모수에 해당하는 발생 횟수(또는 발생률)이다.
• 지수 분포를 이용해 아래를 구할 수 있다.
  • 유저 별 평균 서비스 방문 횟수($\lambda$)가 포아송 분포를 따른다고 했을 떄, 유저 별 7일 이내에 서비스에 재방문할 확률을 구하시오.
• 추가 정보
  • what is exponential distribution

Scipy 코드

# 지난 7일 간의 일 평균 방문 횟수가 2.43회 인 한 명의 유저 기준
rv = sp.stats.expon(1/2.43)

plt.figure(figsize=(20, 10))
n = 5
plt.subplot(1, 2, 1)
xx = np.arange(0, n+1, 0.1)
pdf = rv.pdf(xx)
plt.bar(x=xx, height=pdf, align="center", )
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("지수분포의 확률밀도함수")


plt.subplot(1, 2, 2)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("지수분포의 누적밀도함수")


plt.tight_layout()
plt.show()

감마분포

• 지수 분포가 사건이 1번 발생하는데 걸리는 시간에 대한 분포라면, 감마 분포는 사건이 a번 발생하는데 걸리는 시간에 대한 분포이다.
• 감마 포는 2개의 모수가 있는데,
  • 몇 개의 사건이 발생할 때까지의 시간인가를 결정하기 위해 필요한 사건 발생 횟수 a 가 있다.
    • 사건의 발생 횟수 a 는 형상 모수(shape parameter) 라고 한다.
  • 지수 분포와 마찬가지로 1/$\lambda$ 가 있다.
    • 1/$\lambda$ 는 척도 모수(scale pararmeter) 라고 한다.
• 감마 분포를 이용해 아래를 구할 수 있다.
  • 유저 별 평균 방문 횟수가 포아송 분포를 따른다고 가정할 때, 유저 별로 7일 이내 3번 방문할 확률을 구하시오.
• 감마 분포의 대의적 정의
  • 형상모수 a가 자연수인 경우

\[X \sim Gamma(r, \beta) \ \Leftrightarrow \ X \overset{d}{\equiv} Z_1 + Z_2 + \cdots + Z_n, \ Z_i \overset{iid}{\sim}Exp(\beta)(i=1, \cdots, n)\]

• 추가 정보
  • gamma distribution intuition derivation and examples

Scipy 코드

# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gamma.html#scipy.stats.gamma
# when a = 1 to the exponential distribution, 지수 분포는 감마분포에서 형상 모수가 1인 경우
# 즉, a = 형상 모수  = alpha
# 어떤 사건의 발생률이 2.57이고, 이 사건이 3번 발생할 때까지의 대기시간의 분포

rv = sp.stats.gamma(a=3, scale = 1/2.57)

plt.figure(figsize=(20, 10))
n = 5
plt.subplot(1, 2, 1)
xx = np.arange(0, n+1, 0.1)
pdf = rv.pdf(xx)
plt.bar(x=xx, height=pdf, align="center", )
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("감마분포의 PDF")


plt.subplot(1, 2, 2)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("감마분포의 CDF")


plt.tight_layout()
plt.show()

베타분포

• 아래 정리한 내용은 이 포스팅 의 내용을 요약 정리한 내용입니다.
• 확률 또는 비율과 관련된 확률 분포. 즉, 어떤 사건이 발생할 확률이 x % 이상일 확률이 y%이다 로 해석하는 경우
• 베타 분포의 PDF

\[\frac{x^{\alpha-1}(1-x)^{\beta - 1}}{B(\alpha, \beta)} \ where \ B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}\]

• 베타 분포의 PDF 에 대한 해석
  • 분모의 $B(\alpha, \beta)$는 normalizing 상수 이므로 무시
  • 분자의 x와 1-x 꼴은 이항분포에서 나온 꼴
• 베타 분포의 모수는 2가지 인데 a 또는 b 아니면 $\alpha$ 와 $\beta$ 가 있다.
  • $\alpha$ 을 성공한 횟수로, $\beta$을 실패한 횟수로 생각할 수 있음
• 베타 분포를 이용해 아래와 같은 문제에 답을 할 수 있다.
  • 누군가에게 데이트 신청 했을 때, 2번을 성공 했고, 8번은 실패했다고 가정하자.
  • 내가 데이터 신청 했을 때, 성공 확률이 50%가 넘을 확률은? 1.95%로 매우 낮다.

# 총 7번의 시도 중 3번 성공하고 4번 실패하는 경우
rv = sp.stats.beta(a=3, b=4)

plt.figure(figsize=(20, 10))
n = 5

plt.subplot(1, 2, 1)
xx = np.arange(0, 1, 0.1)
pdf = rv.pdf(xx)
plt.bar(x=xx, height=pdf, align="center", )
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("베타분포의 PDF")


plt.subplot(1, 2, 2)
cdf = rv.cdf(xx)
plt.bar(x=xx, height=cdf, align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("베타분포의 CDF")


plt.tight_layout()
plt.show()

Reference

• 서적
  • 피터 브루스, 앤드루 브루스, [데이터 과학을 위한 통계], 한빛미디어
  • 김우철, 수리통계학, 민영사
• 블로그
  • https://datascienceschool.net/intro.html
  • https://towardsdatascience.com/beta-distribution-intuition-examples-and-derivation-cf00f4db57af