Dongsu Kang

Data Analyst

순열 검정(Permutation Test)

2 minute read

순열 검정(Permutation Test)을 왜 알아야 하는가

  • 사실 이 링크 페이지에서만큼 정성스럽게 잘 설명할 자신이 없어서, 여기를 읽어보는 것이 좋을 것 같다.
  • 내 나름대로의 설명을 덧붙여보자면
    • 일반적으로 두 집단의 차이를 비교할 때는 평균을 비교한다. 하지만, 분산의 개념을 안다면, 평균끼리의 비교로 어느 것이 더 높고, 또 낮다고 말할 수 없다는 것을 알 것이다.
    • 그래서 모수 통계학에서는 두 집단의 차이를 비교할 때의 가설 검정법이 정리되어 있다. 평균끼리의 비교는 대표적으로 T 검정을 이용한다.
    • 하지만, 이러한 검정법을 올바르게 이용하기 위해서는, 검정에서 요구하는 가정을 만족해야 한다. 가령, T 검정의 경우, 표본 집단들의 정규성, 등분산성, 독립성이 가정되어야 한다.
      • 여기서, 정규성은 표본의 수가 적당히 클 경우, 중심극한정리에 의해 만족한다고 가정할 수 있다.
      • 단, 이 경우는 t 분포를 이용하여 검정하는 것이 아니라 표준정규분포 를 이용하여 검정한다.
    • 요즘은 데이터가 많은 시대이니, 위와 같은 흐름으로 정규성을 해결하였다고 해도, 결국 등분산성을 만족시키기는 쉽지 않다.
    • 또한, 모집단에 대한 정규성과 집단들의 등분산성을 모두 만족한다고 해도, 이를 확인하는 절차가 까다롭다.
    • 또, 만약, 위와 같은 절차를 거치지 않고도 검정을 할 수 있다면 써보고 싶지 않을까? 이럴 때 사용할 수 있는 것이 순열 검정(Permutation Test)이다.

순열 검정(Permutation Test)이란?

  • 순열 검정을 하는 법은 간단하다.
    1. 만약 두 집단 A, B가 각각 1000개, 2000개 씩 있고, 두 집단의 평균의 차이가 있는지 확인해보고 싶다고 가정한다.
      • 이 경우, 귀무가설은 A 집단과 B 집단의 평균의 차이가 없다로 설정한다, 대립가설은 A 집단과 B집단의 차이가 있다로 설정한다.
    2. A, B 집단을 모두 섞어 총 3000개의 데이터 셋을 만든다.
    3. 이 중 1000개를 뽑아 A집단으로 설정하고, 평균을 구하고 기록한다.
    4. 나머지 2000개를 B 집단으로 설정하고, 평균을 구하고 기록한다.
    5. 3,4 번의 과정을 N 번 반복하고, 이를 분포로 시각화 한다.
    6. 처음 가지고 있던 원래의 A, B 집단의 데이터의 평균의 차이가 5번 과정에서 결과로 나온 분포에서 어느 정도의 위치를 가지는지 확인한다.
  • 해당 분포에서 얼마나 극단적으로 위치했느냐에 따라서 두 집단의 차이가 우연인지 아닌지를 주장할 수 있다.
  • 가설 검정은 결국 부트스트랩방법과 연관이 있다.
  • 위 방법을 통해, 평균의 차이 뿐만 아니라, 비율의 차이 등에 대해서도 검정이 가능하다.

파이썬 코드

아래는 비율의 차이에 대한 검정의 파이썬 코드 예시이다.

sample_click_ratio_list = list()

n = 10000

# 순열 검정 부분
for _ in range(n) : 
    
    sample_A_user_list = data.sample(n=size_of_A)["userId"].unique()
    sample_B_user_list = data[~data["userId"].isin(sample_A_user_list)]["userId"].unique()

    sample_A_data = data.query("userId in @sample_A_user_list")
    sample_B_data = data.query("userId in @sample_B_user_list")
    
    sample_A_conversion = (sample_A_data["is_viewed"].sum() / sample_A_data.shape[0]).round(4)
    sample_B_conversion = (sample_B_data["is_viewed"].sum() / sample_B_data.shape[0]).round(4)
    
    diff = sample_A_conversion - sample_B_conversion
    sample_click_ratio_list.append(diff)

# 시각화 부분
# 분포 확인
plt.figure(figsize=(12, 6))
ax = plt.hist(sample_click_ratio_list, bins=20, alpha=0.8)

plt.title(label=f"distribution of sample click ratio differences (Number of trials: {n:,})")
plt.xlabel(xlabel="sample click ratio difference")
plt.ylabel(ylabel="frequency")

sigma_1_left = np.mean(sample_click_ratio_list) - np.std(sample_click_ratio_list)
sigma_1_right = np.mean(sample_click_ratio_list) + np.std(sample_click_ratio_list)

sigma_2_left = np.mean(sample_click_ratio_list) - (np.std(sample_click_ratio_list) * 2)
sigma_2_right = np.mean(sample_click_ratio_list) + (np.std(sample_click_ratio_list) * 2)


plt.axvline(x=0.0077, ymin=0, ymax=1, color="b", ls="-")

plt.axvline(x=sigma_1_left, ymin=0, ymax=1, color="g", ls="--")
plt.axvline(x=sigma_1_right, ymin=0, ymax=1, color="g", ls="--")

plt.axvline(x=sigma_2_left, ymin=0, ymax=1, color="r", ls="--")
plt.axvline(x=sigma_2_right, ymin=0, ymax=1, color="r", ls="--");

파이썬 코드 결과

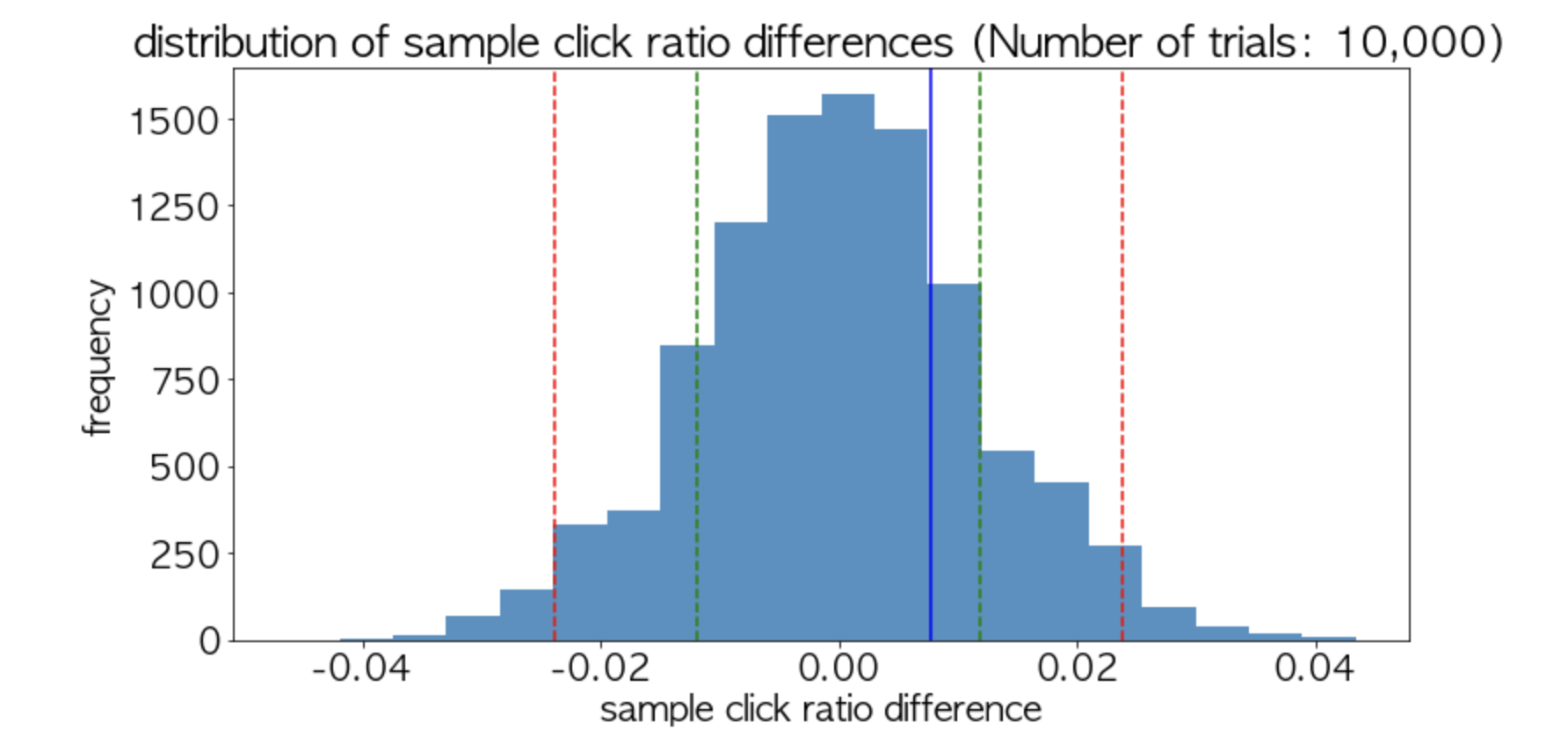
  • 해석
    • 실제 결과치는 진한 파랑색이며, 초록 점선은 1표준 편차 이내, 빨간 점선은 2표준편차 이내의 거리를 뜻한다.
    • 해당 분포에서 진한 파랑색 선은 분포의 거의 중심에 위치하며, 이보다 큰 경우의 값이 발생하는 경우가 충분히 많음을 볼 수 있다.
    • 따라서, 이 차이는 우연으로 충분히 발생할 수 있는 수치이며, 이는 통계적으로 유의미하다고 얘기할 수 없다.(즉, p-value 가 귀무가설을 기각할 수 없을만큼 충분히 크다)

Reference

  • 서적
    • 피터 브루스, 앤드루 브루스, [데이터 과학을 위한 통계], 한빛미디어
  • 블로그

You may also enjoy